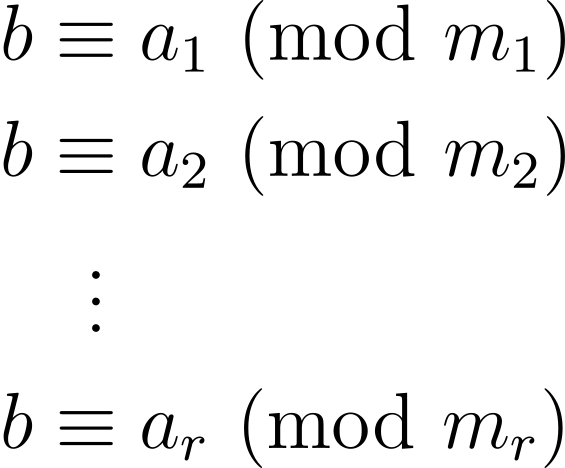Fermat’s Little Theorem For any prime p and any integer a,
![]()
If p doesn’t divide a, then this is equivalent to
![]()
Euler’s Theorem
This is a generalization of Fermat’s Little Theorem. Define the totient function Φ on the positive integers to be Φ(n) = the number of positive integers between 1 and n (inclusive) that are coprime to n. Then for any coprime positive integers a and n, Euler’s Theorem states that
![]()
Wilson’s Theorem
For any integer p > 1, (p – 1)! + 1 is divisible by p if and only if p is prime.
Chinese Remainder Theorem
If m₁, m₂, …, mᵣ are pairwise coprime positive integers > 1 and a₁, a₂, …, aᵣ are any integers, there is exactly one integer b between 0 and m₁ m₂ ∙∙∙ mᵣ – 1 (inclusive) such that