For any real number x, we have x² ≥ 0. Equality holds precisely when x = 0.
This simple inequality has interesting consequences. For instance:
Arithmetic Mean – Geometric Mean inequality (AM-GM)
For any positive reals a₁, a₂, …, aₙ,
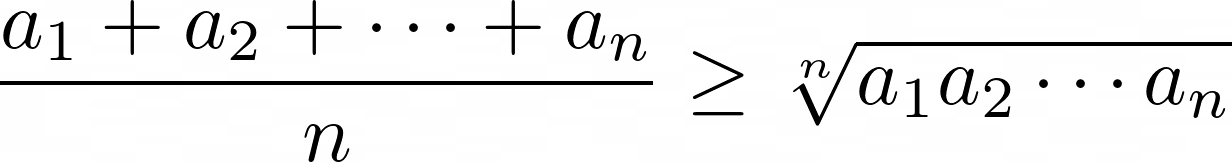
Equality holds precisely when the aᵢs are all equal.
The case of n = 2 can be seen by considering
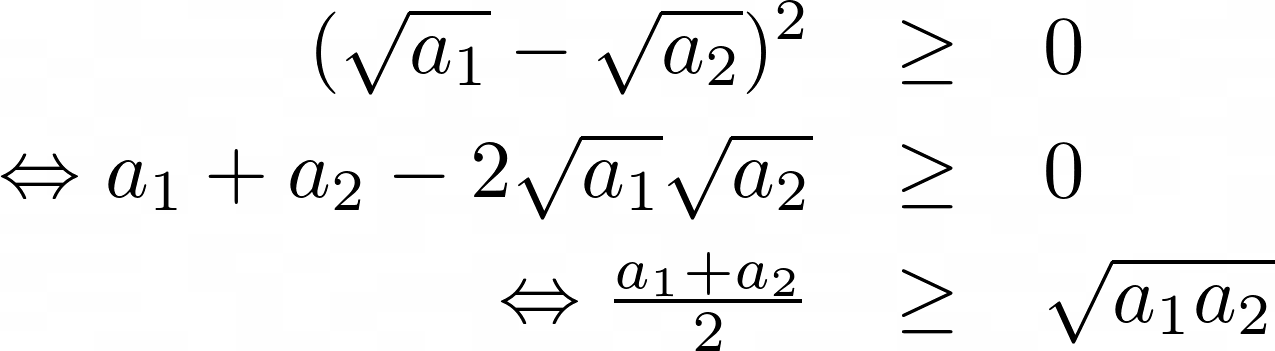
(SMO 2013) Let x₁ and x₂ be real numbers satisfying x₁x₂ = 2013. What’s the minimum value of (x₁ + x₂)²?
Solution: By AM-GM,
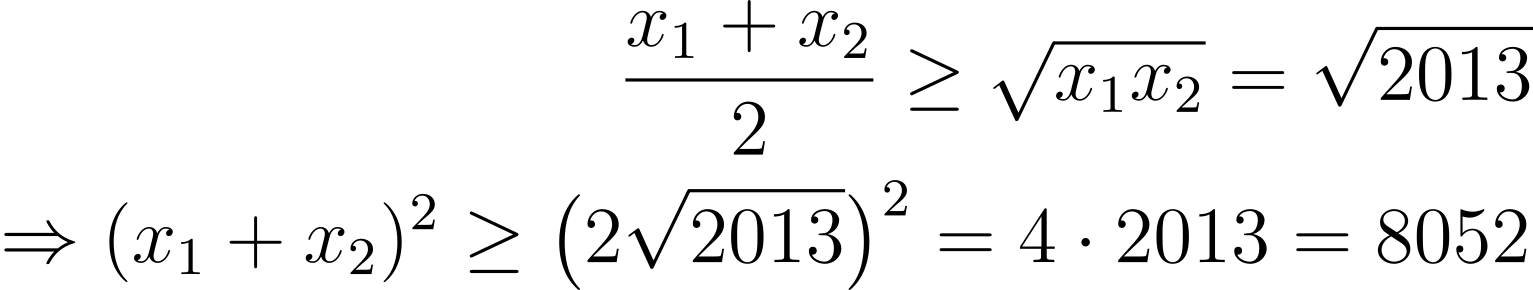
Equality holds when x₁ = x₂ = √2013, hence the minimum value is 8052.
Weighted Power Mean Inequality Let a₁, a₂, …, aₙ and w₁, w₂, …, wₙ be positive reals with w₁ + w₂ + … + wₙ = 1. For any real number r, define
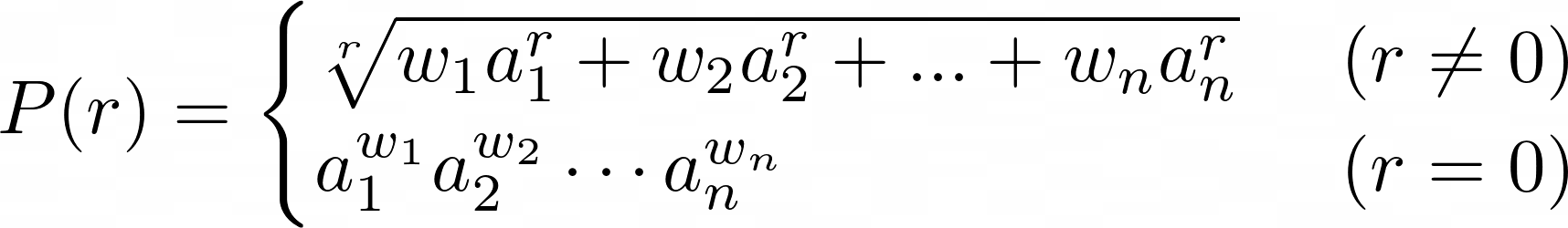
If r > s, then P(r) ≥ P(s), with equality precisely when all the aᵢs are equal.
Rearrangement Inequality Let a₁ ≥ a₂ ≥ … ≥ aₙ and b₁ ≥ b₂ ≥ … ≥ bₙ be two non-increasing sequences of reals of the same length. If c₁, c₂, …, cₙ is any rearrangement of b₁, b₂, …, bₙ, then
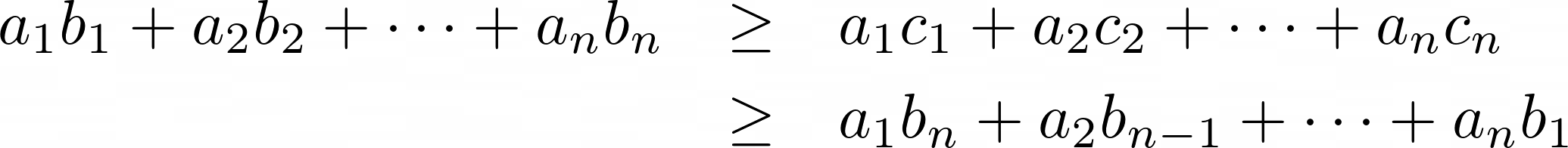
Cauchy-Schwarz Inequality For any real aᵢ s and bᵢ s, we have
![]()
Equality holds if and only if a₁/b₁ = a₂/b₂ = … = aₙ/bₙ

