A simple and powerful technique to solve algebra and number theory problems is to try to factor expressions. Here are some examples:

(2010 SMO Senior)     Determine the odd prime number p such that the sum of digits of the number p⁴ – 5p² + 13 is the smallest possible.

The expression is similar to p⁴ – 5p² + 4, which can be factored as (p² – 1)(p² – 4) and even further. Using this idea, we write

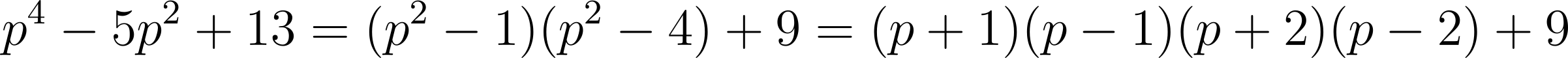
When p = 3, p⁴ – 5p² + 13 = 49 and the sum of its digits is 13. When p = 5, p⁴ – 5p² + 13 = 513 and the sum of its digits is 9. When p > 5, observe that p – 2, p – 1, p, p + 1 and p + 2 are five consecutive integers. Since p cannot be a multiple of 5, one of the others must be. Also, p + 1 and p + 2 are two consecutive integers, so at least one of them must be even. Hence 10 is a factor of (p – 2)(p – 1)(p + 1)(p + 2) and so the last digit of (p – 2)(p – 1)(p + 1)(p + 2) + 9 is 9. Together with the other digits, the sum of its digits must be greater than 9. Hence p = 5 gives the smallest digit sum.

Polynomial Long Division

Given two polynomials A(x) and B(x), there exist unique polynomials Q(x) and R(x) with the degree of R(x) < degree of B(x) such that

B(x) is a factor of A(x) if and only if R(x) = 0.

To find Q(x) and R(x), you can perform polynomial long division.

Sometimes you can’t factor an expression perfectly, but finding the remainder after dividing by a factor can still tell you something about the expression.