Often when solving geometry problems, it’s useful to construct additional points and lines.
(NMOS 2011 Special Round Q14) In the figure below, BCD is a straight line, ∠BCA = 69°, ∠ADB = 42° and AD = BC. Find ∠ABC (in degrees).
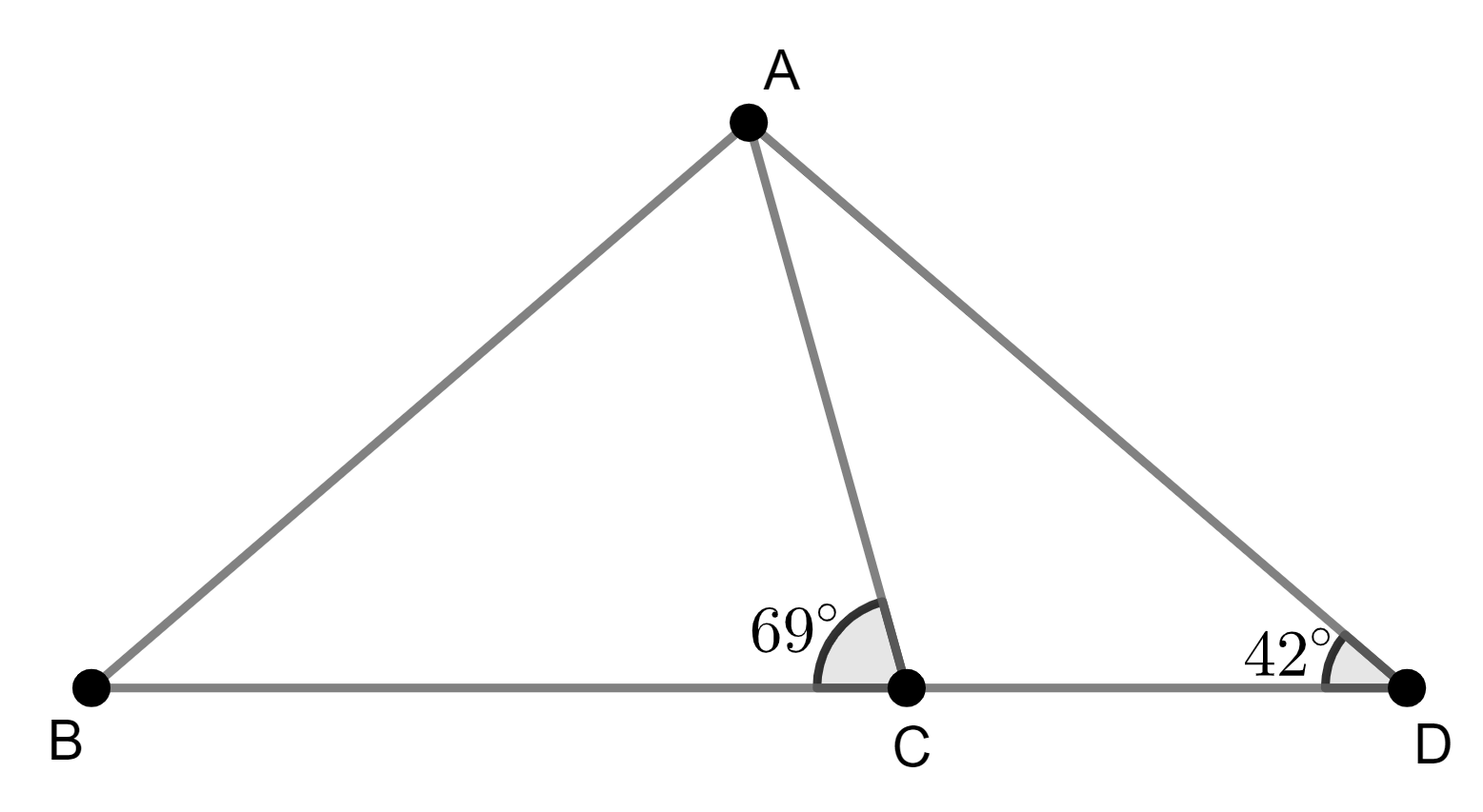
From a quick investigation of the diagram, you can easily see that ∠ACD = 111° = 69° + 42°, which suggests you should make use of this relationship somehow. You can place a 42° angle adjacent to a 69° by constructing a point C‘ such that ΔBCC’ is congruent to ΔADC.
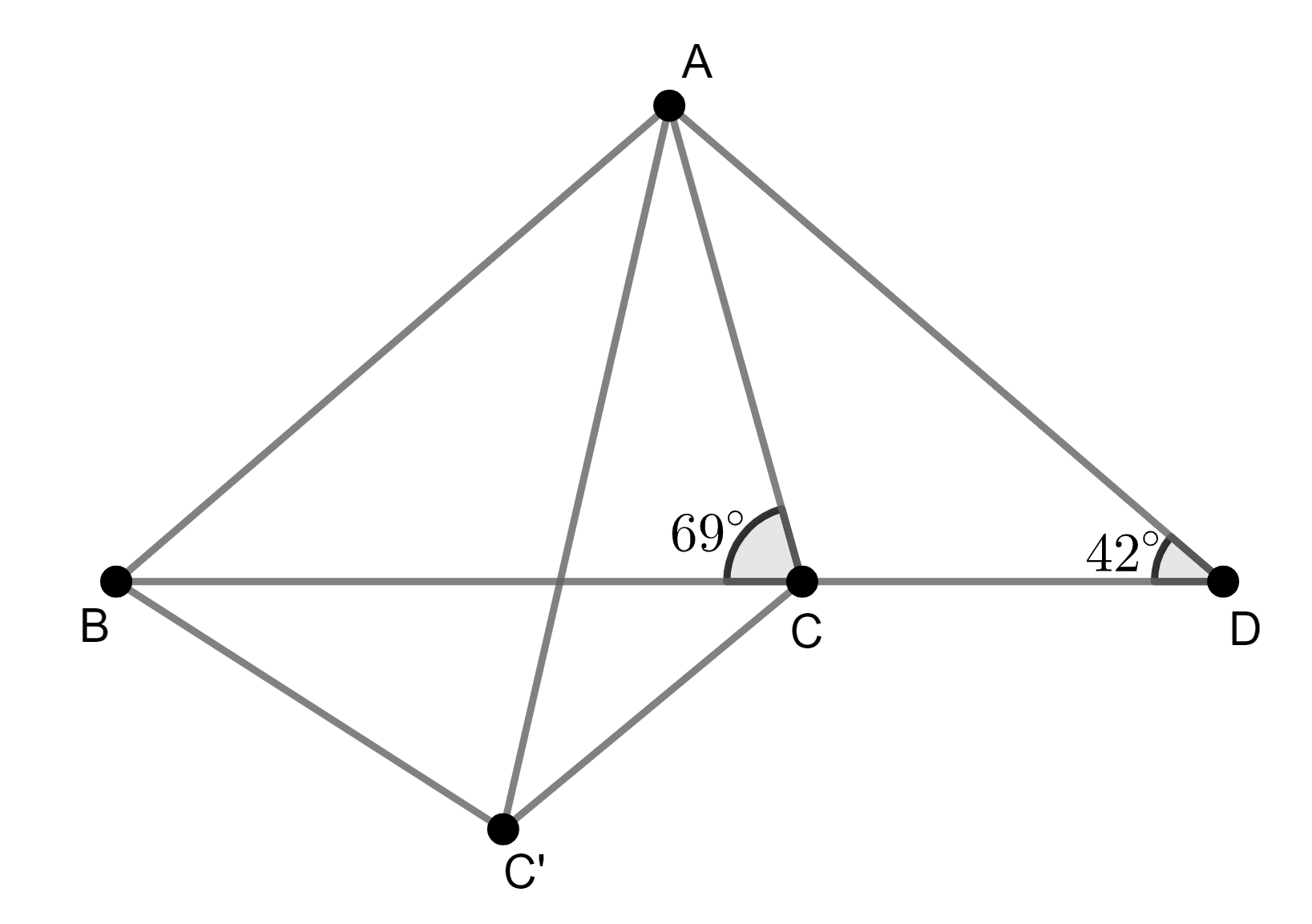
BC = AC and ∠BC’C = ∠C’CA, hence ABC’C is a trapezium and must be cyclic. Thus ∠ABC = ∠AC’C = ∠ADC = 42°.

