A (univariate) polynomial is an expression of the form
![]()
where the aᵢ s are constants (aₙ ≠ 0) and x is a variable. The aᵢ s are called the coefficients of the polynomial. n is the degree of the polynomial. aₙ is the leading coefficient and a₀ is the constant term. If the leading coefficient is 1, then the polynomial is a monic polynomial.
A root of the polynomial is a value for x such that P(x) = 0.
The Fundamental Theorem of Algebra states that every polynomial of degree n will have n roots. Note that the roots need not be real and there may be repeated roots. If r₁, r₂, …, rₙ are the roots of P(x), then
![]()
Expanding the product on the right hand side and comparing with the coefficients of P(x) gives

![]()

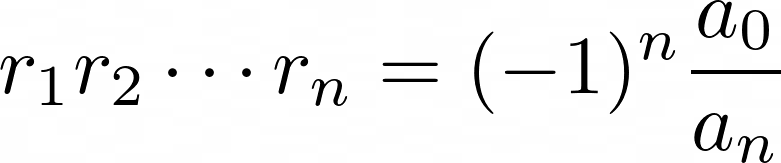
The expressions on the left hand sides are called the elementary symmetric polynomials in the rᵢ s
(SMO 2011) Let P(x) be a polynomial of degree 2010. Suppose P(n) = n/(1 + n) for n = 0, 1, 2, …., 2010. Find P(2012)
Solution: n/(1 + n) isn’t a polynomial, which makes it harder to understand. Consider the expression (1 + n)P(n) – n, which is a degree 2011 polynomial. It has 2011 distinct roots n = 0, 1, 2, …, 2010, hence it must be of the form an(n – 1)(n – 2)…(n – 2010) for some constant a. Substituting n = -1, we find that a = 1/2011! . Substituting n = 2012, we find that P(n) = 0.
(SMO 2012 Open) The product of two of the four roots of the quartic equation x⁴-18x³+kx²+200x-1984=0 is -32. Determine the value of k.
Let a, b, c, d be the four roots of the quartic, with ab = -32. Then
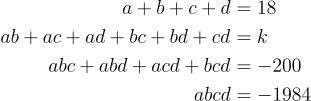
Hence cd = -1984/-32 = 62. -200 = cd(a + b) + ab(c + d) = 62(a + b) – 32(c + d). Solving this together with 18 = (a + b) + (c + d) gives a + b = 4 and c + d = 14. Then k = -32 + ac + ad + bc + bd + 62 = (a + b)(c + d) + 30 = 86.

